Representación del lazo vectorial de eslabonamientos

 

Un enfoque alternativo de análisis para la posición de eslabonamientos es crear un lazo vectorial (o lazos) alrededor del eslabonamiento.* Este enfoque ofrece algunas ventajas en la síntesis de eslabonamientos. Los eslabones se representan como vectores de posición. El mismo eslabonamiento de cuatro barras, pero ahora los eslabones están dibujados como los vectores de posición del lazo vectorial. Este lazo se cierra en sí mismo haciendo que la suma de los vectores con respecto al lazo sea cero. Las longitudes de los vectores son las longitudes de los eslabones, las cuales se conocen. La posición actual de eslabonamiento está definida por el ángulo de entrada como un mecanismo de un GDL. Se quieren determinar los ángulos desconocidos Para hacer esto se necesita representar los vectores una notación conveniente.

 

 |

ANÁLISIS GRÁFICO DE POSICIÓN DE ESLABONAMIENTOS

Para cualquier eslabonamiento con un GDL, tal como uno de cuatro barras, sólo se necesita un parámetro para definir completamente las posiciones de todos los eslabones.

El parámetro que normalmente se escoge es el ángulo del eslabón de entrada. Este se muestra como θ2 . Se quiere encontrar θ3 y θ4, se conocen las longitudes de los eslabones. Observe que de manera consistente se numerará al eslabón de fijación

 

El análisis gráfico de este problema es trivial y puede hacerse usando sólo geometría de bachillerato. Si se dibuja el eslabonamiento cuidadosamente a escala, con regla, compás y transportador en una posición en particular (dada entonces sólo es necesario medir los ángulos de los eslabones 3 y 4 con el transportador. Observe que todos los ángulos de los eslabones se miden a partir del eje X positivo se creó un paralelo al sistema local de ejes sistema global en el punto A para medir La precisión de esta solución gráfica dependerá de su cuidado y habilidad para dibujar, y de la fineza del transportador usado. No obstante, se puede encontrar una solución rápida aproximada para cualquier posición. 

 

 

 

Evidencias de clase del dia 04/03/21

 

Evidencias de clase del dia 05/03/21

 

Horizontal Slider

 

Evidencias de clase 

Los siete problemas del milenio.

 

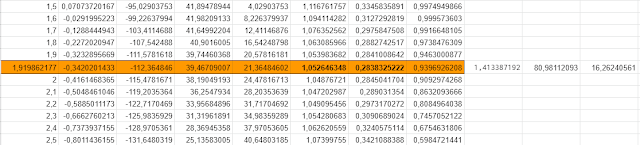
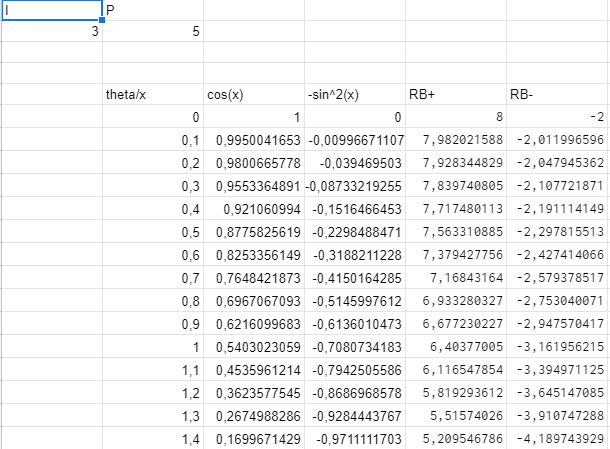
US$1 millón por resolver un problema matemático.

La cuantía de la recompensa permite imaginar la complejidad de los llamados Problemas del Milenio, una lista con los siete desafíos más importantes sin resolver publicada en el año 2000 por el Instituto Clay de Matemáticas de Cambridge, Estados Unidos.

El premio es suculento... pero la tarea no es fácil. Hasta ahora, solo uno ha sido resuelto de manera oficial.

El pasado mes de septiembre, el británico Michael Atiyah aseguró haber solucionado el problema de la "hipótesis de Riemann" al hallar una fórmula con la que predecir el siguiente número primo dentro de una serie de cifras.

Hipótesis de Riemann: Michael Atiyah, el "genio" de 89 años que asegura haber resuelto uno de los mayores problemas matemáticos de la historia

Pero antes de poder recibir el premio, su teoría debe ser publicada por una revista científica de prestigio mundial. Dos años después, si la teoría es aceptada por la comunidad matemática, tendrá que recibir el visto bueno de dos comités independientes de expertos del Instituto Clay.

1. El problema de P frente a NP

"P frente a NP" aspira a demostrar o refutar la creencia de que hay problemas para los que, por su complejidad, es más difícil encontrarles una solución que comprobar si esa solución es correcta.

Los problemas P (polinómicos) son los que se pueden resolver en un tiempo razonable. Los problemas NP (no deterministas en tiempo polinómico) son aquellos que, aunque sea difícil encontrarles solución, una vez hallada se puede comprobar en un tiempo razonable que es correcta.

Si se puede encontrar fácilmente una solución, esta también se podrá verificar de manera sencilla, por lo que todo problema P es también NP.

Lo que se desconoce es si hay algún problema NP que no sea P. Los expertos confían en que así sea, pero de momento nadie ha sido capaz de demostrarlo.

2. La conjetura de Hodge

Algunos matemáticos aseguran que este problema es el más difícil de explicar al público en términos que no resulten demasiado técnicos.

La conjetura de Hodge está relacionada con la geometría algebraica, que estudia los lugares geométricos que se pueden definir por polinomios como circunferencias o parábolas.

Con el paso del tiempo, sin embargo, algunas propiedades de estos conjuntos comenzaron a ser aplicadas a cosas que no tienen una interpretación geométrica. Una de ellas es lo que se conoce como un "ciclo de Hodge".

3. La conjetura de Poincaré

Este problema es el único que hasta el momento fue solucionado oficialmente. El logro fue del matemático ruso Grigori Perelman en 2006, quien sorprendió al rechazar el premio tras asegurar que no era ningún héroe ni quería ser expuesto de manera masiva.

"El genio que no quería un millón de dólares"

La conjetura de Poincaré era considerada una de las hipótesis matemáticas más importantes y difíciles de demostrar.

En topología, la superficie de una esfera bidimensional se caracteriza por ser la única superficie simplemente conexa, compacta y cerrada (sin límites).

La conjetura, que se transformó en teorema después de que la resolución de Perelmán fuera aceptada, establece que esta afirmación es también válida para esferas tridimensionales.

4. La hipótesis de Riemann

La hipótesis de Riemann se centra en la distribución de los números primos, aquellos indivisibles por cualquier otro número que no sea 1 ni ellos mismos.

El matemático alemán Bernd Riemann sugirió que la distribución de estos números está estrechamente relacionada con el comportamiento de la llamada "función zeta de Riemann".

5. Yang-Mills y el salto de masa ("mass gap")

Distintos experimentos descubrieron la existencia de un mass gap (traducido en español como "salto de masa" o "intervalo másico") en la solución a la teoría de Yang-Mills, la cual estableció las bases de la teoría de las partículas elementales de la materia y en cuya versión cuántica describen partículas sin masa (gluones).

El uso exitoso de esta teoría para describir las fuertes interacciones de las partículas elementales depende de ese "salto de masa", una propiedad mecánica cuántica según la cual las partículas cuánticas tienen masas positivas, aunque las ondas clásicas viajan a la velocidad de la luz.

El refugiado que ganó el "Premio Nobel de las Matemáticas" (y le robaron la medalla)

Los matemáticos que ayudaron a Einstein y sin los cuales la teoría de la relatividad no funcionaría

Aunque esta propiedad fue confirmada por simulaciones por computadora, aún no se logró entender desde un punto de vista teórico.

El problema consiste en determinar de manera rigurosa la existencia de una teoría de Yang-Mills cuántica que pueda explicar este fenómeno. Es decir, si —como muchos expertos creen— todas las partículas de esta teoría (los gluones) tienen masa o no.

6. Las ecuaciones de Navier-Stokes

Estas ecuaciones describen el movimiento de fluidos como líquidos y gases que gobiernan la atmósfera terrestre, las corrientes del océano o el flujo alrededor de vehículos o proyectiles.

Pese a que desde su formulación en el siglo XIX describen adecuadamente tanto el flujo turbulento (el que se da de manera caótica) como laminar (no turbulento), sigue sin existir una explicación rigurosa de cómo un fluido pasa de tener un flujo regular a uno turbulento.

Los científicos tratan de conseguir una mejorada teoría matemática sobre la dinámica de fluidos que ayude a entender el fenómeno de la turbulencia y desbloquear los muchos secretos ocultos que aún permanecen en las ecuaciones de Navier-Stokes.

Matemáticos y físicos creen que esto nos ayudaría a mejorar nuestro conocimiento sobre la formación de olas en el mar o turbulencias en el aire y, lo que es aún más importante, poder predecirlas mejor.

7. Conjetura de Birch y Swinnerton-Dyer

La conjetura de Birch y Swinnerton-Dyer, que une geometría algebraica y teoría de números, pide estudiar las soluciones racionales a ecuaciones que definen una curva elíptica.

Las curvas algebraicas se clasifican según su género, siendo las más sencillas las de género cero o curvas racionales (que tienen ninguna o infinitas soluciones racionales).

El problema, sin embargo, está en demostrar un criterio que distinga qué curvas de género 1 (también llamadas elípticas) tienen un número finito o infinito de soluciones racionales.

CUESTIONARIO ANÁLISIS DE POSICIÓN Y DESPLAZAMIENTO

1.-¿Cuando ocurre un movimiento?

Un mecanismo es estudiar su movimiento. El movimiento ocurre cuando se modifican la posición de los eslabones y los puntos de referencia del mecanismo.

2.-¿Que es una manivela?

Una manivela,  es un elemento que tienen ciertas máquinas para conferir, de forma manual, un movimiento rotatorio. Esto quiere decir que las manivelas forman parte de un mecanismo que permite la transmisión de movimiento.

3.-¿Qué es un cigüeñal?

Un cigüeñal es un eje giratorio que convierte el movimiento alternativo de un pistón en un movimiento giratorio. Se usa comúnmente en motores de combustión interna para realizar dicha operación, y permite que las ruedas impulsen el vehículo. 

4.-¿Que es el desplazamiento?

El desplazamiento es el producto final del movimiento. Se trata de un vector que representa la distancia entre la posición inicial y la posición final de un punto o un eslabón.

5.-¿Que es el desplazamiento  lineal?

Es la distancia lineal recta entre la posición inicial y la posición final de un punto.

6.-¿Que es el desplazamiento angular y su formula?

Es la distancia angular entre dos configuraciones de un eslabón giratorio. Es la diferencia entre la posición angular inicial y la posición angular final del eslabón. su formula es: 

7.-¿Cuando un eslabón se reposiciona es cierto determinar la posición de los demás?

Es cierto, Una vez reposicionado el eslabón impulsor, se debe determinar la posición de los demás eslabones. Para hacerlo, se tienen que construir las trayectorias posibles de todos los eslabones conectados a la bancada.

8.-¿Que son los grados de libertad?

Los grados de libertad de un mecanismo determinan el numero de eslabones impulsores independientes.

9.-¿Que es un eslabón fijo?

No. de los eslabones no tiene movimiento, denominándose eslabón fijo o tierra. Se denomina eslabón también a cada uno de los componentes de una cadena.

10.-¿Porque se le llama bancada?

La bancada es el órgano que constituye la parte inferior del motor, sirve de soporte para las piezas rotantes y como pared de contención para el aceite lubricante.

QUE ES ESLABONAMIENTO

Es un termino se refiere como la acción y resultado de eslabonar o de eslabonarse, en acoplar, unir, juntar o empalmar unos eslabones con otros elementos hasta formar una cadena. Encadenar, engarzar o vincular las partes de un discurso o una cosa con otra. Encadenar, engarzar o vincular las partes de un discurso o una cosa con otra. La teoría de los eslabonamientos hacia atrás y hacia adelante de Hirschman procura mostrar cómo y cuándo la producción de un sector es suficiente para satisfacer la escala mínima necesaria que convierte en atractiva la inversión en otro sector que abastece al primero (eslabonamiento hacia atrás) o procesa su producción (eslabonamiento hacia adelante) (Ramos, 1999). Hirschman (1970) considera que al hablar de los efectos de eslabonamiento que emanan de una industria hacia otra industria, no sólo se hace referencia a la importancia potencial del efecto de eslabonamiento (por ejemplo en términos de la producción neta de las nuevas industrias que pudieran aparecer), sino también a la fuerza del efecto (es decir, a la probabilidad de que estas industrias surjan). El efecto total podría medirse sumando los productos de estos dos elementos. La actividad inicial daría así lugar a una oleada de inversiones que no sólo multiplicarían el efecto inicial sino que generarían actividades cada vez más diversificadas y, por lo tanto, menos dependientes del impulso originario (Gorenstein, Viego y Burachik, 2006). Los países subdesarrollados, cuyas economías se basan fundamentalmente en actividades primarias (agricultura y minería), se caracterizan por la falta de interdependencia y eslabonamiento. Por definición, toda producción primaria excluye cualquier eslabonamiento anterior sustancial, siendo a su vez débiles los efectos de eslabonamiento posterior (la producción no se industrializa en el país sino que se exporta en forma de commodities). Las llamadas “actividades incrustadas de exportación” (producción y exportación de bienes en forma aislada del resto de la economía) se caracterizan por los escasos eslabonamientos directos. Si bien estos enclaves pueden generar algún tipo de eslabonamiento posterior, resulta difícil que abandonen su condición de incrustación. De todos modos, podrían financiar importaciones que pueden llegar a ser agentes poderosos de desarrollo (Hirschman, 1970).

Corredera diagonal (FreeCAD)

Clase del día 03/03/2021

 Corredera diagonal. 

Vital Cocolot Jose Artemio 

Teorema de Fermat

 

El pasado 15 de marzo del 2016 se entregó el premio Abel, el premio Nobel de matemáticas, a Andrew Wiles por haber confirmado una conjetura matemática cuya validez no había podido ser demostrada desde que se propuso en 1642.

Esta conjetura nació de la mano del jurista y matemático Pierre de Fermat que, mientras leía su copia del libro 'Arithmetica', un texto matemático escrito por Diofanto de Alejandría en el siglo III a.C., en sus márgenes iba anotando problemas y conjeturas que se le ocurrían sobre la marcha. En los siglos que se sucedieron tras su muerte, otros matemáticos fueron abordando y solucionando cada uno de los problemas que Fermat había garabateado… Hasta que sólo quedó uno por resolver:

“No existe ningún número entero positivo mayor que 2 que satisfaga la ecuación an + bn = cn”

Donde “n” es dicho número, por supuesto. Esta conjetura fue bautizada con el nombre de “el último teorema de Fermat”, precisamente porque era la última proposición de este autor que nadie había podido refutar o verificar.

Fermat y Pitágoras

En algún punto de nuestras vidas, todos hemos usado el teorema de Pitágoras, la fórmula que relaciona la longitud de los catetos de un triángulo con la longitud de su hipotenusa. Ese es precisamente el caso del teorema de Fermat cuando n=2. Pero, en este caso, la igualdad no tiene ningún misterio, porque sabemos que se cumple para una gran cantidad de combinaciones de números distintas. Por ejemplo, sabemos que 32 + 44 = 52 (9 + 16 =25).

 

Pero, ¿y si n=3? ¿Existe alguna combinación de números que, elevados al cubo, la suma de dos de ellos sea igual al cubo de un tercer número? ¿Y qué pasa con los infinitos exponentes mayores que 3? Pues, según Fermat, no existiría ninguna combinación de números que cumpla esta igualdad con cualquier número entero positivo superior a 2.

 

Pero no basta con decir las cosas para que se hagan realidad. Las proposiciones matemáticas se tienen que poner a prueba para demostrar su validez y, en el caso de Fermat, había que comprobar si es verdad que no existe ninguna combinación que cumpla su igualdad y que, por tanto, tenía razón, o si, por el contrario, sí que existe al menos una combinación que la cumple, lo que demostraría que su afirmación era falsa. Pero, aunque el concepto pueda parecer sencillo, comprobar si Fermat tenía o no razón no era una tarea fácil.

Cómo demostrar un teorema

Básicamente, si quieres comprobar la validez de un teorema matemático de este estilo, tienes dos opciones:

 

1. Ir probando combinaciones de números hasta encontrar un ejemplo que lo contradiga, con lo que demostrarías con toda seguridad que la proposición de Fermat es falsa.

 

2. Demostrar usando la lógica matemática si, por el motivo que sea, la afirmación es verdadera o falsa.

 

A primera vista, podría parecer que el camino más sencillo sería encontrar un ejemplo que refute el teorema de Fermat. Pero hay tener en cuenta que, si el teorema resultara ser verdadero, entonces te pasarías toda la vida metiendo números en la fórmula sin encontrar nunca un ejemplo que lo contradijera.

Mejor usar la lógica

Y eso es precisamente lo que hizo Andrew Wiles.

Nacido en 1953, Wiles se había encontrado por primera vez con el teorema de Fermat a los 10 años, cuando encontró un libro sobre éste en la librería mientras volvía del colegio. El teorema le fascinó porque, pese a ser tan simple que lo podía entender él mismo con 10 años, era tan complejo que nadie lo había resuelto en sus tres siglos de historia. Muchos matemáticos incluso sostenían que era imposible de resolver.

Wiles sabía que las habilidades matemáticas que tenía en ese momento no le servirían para resolver el teorema, de modo que lo olvidó hasta 1986.

El secreto para resolver este teorema estaba en la geometría, concretamente en la representación matemática de las curvas elípticas y en unas entidades matemáticas llamadas formas modulares, que son unas funciones muy simétricas y abstractas que existen en el plano de los números imaginaros (aquellos que incluyen la raíz cuadrada de -1).