INTRODUCCION A LOS NUMEROS COMPLEJOS

 

Un número complejo $z$ se define como un par ordenado de números reales:

$$z=\left(a,b\right)cona,b\in R$$

donde el primer elemento del par ordenado se llama parte real del número complejo, y el segundo elemento se llama parte imaginaria:

$$Re\left(z\right)=a$$

$$Im\left(z\right)=b$$

En los números complejos se definen las siguientes operaciones:

$$\left(a,b\right)+\left(c,d\right)=\left(a+c,b+d\right)$$

$$\left(a,b\right).\left(c,d\right)=\left(ac–bd,ad+bc\right)$$

Con estas operaciones, puede demostrarse que el conjunto de los números complejos tiene las mismas propiedades que los reales con la suma y el producto. No nos extenderemos desarrollando esta cuestión algebraica porque en la práctica lo usual es operar con otras expresiones de los números complejos, como veremos a continuación.

Podemos identificar de manera natural los complejos de parte imaginaria nula con los números reales:

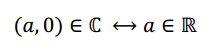
Por otra parte, los números de parte real nula: $z=\left(0,b\right)$ se denominan imaginarios puros. Se define la unidad imaginaria:

$$i=\left(0,1\right)unidadimaginaria$$

Podemos entonces deducir otra forma de expresar un número complejo:

$$z=a+biformabinómica$$

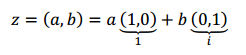
Observación: en algunos textos de Física y de Ingeniería la unidad imaginaria se designa como $j$ , para no confundir con la $i$ que suele indicar la intensidad de corriente eléctrica.

Suma y diferencia de números complejos

La regla para sumar o restar dos números complejos  y  es sumar/restar parte real de uno con parte real del otro y parte imaginaria de uno con parte imaginaria del otro.

 

Cuando se tienen suma y resta combinadas de varios números complejos, se suman y/o restan las partes reales con las partes reales y las partes imaginarias con las partes imaginarias.

https://www.superprof.es/apuntes/escolar/matematicas/aritmetica/complejos/numeros-complejos-resumen.html