El criterio de Grashof
Nos dice que el mecanismo articulado
más simple para el movimiento controlado de un grado de libertad es el
eslabonamiento de cuatro barras. Es de los dispositivos que mas se encuentran
en maquinaria.
Un aspecto que se debe tomar en
cuenta es su versatilidad que permite los diferentes tipos de movimientos que
puede generar.
Un ejemplo de mecanismo de cuatro
barras se muestra en la figura 1.
 |
| Figura 1. Mecanismo de un sistema limpiador para el cristal trasero de un automóvil [1]. |
La sencillez es una marca
distintiva del buen diseño. La menor cantidad de partes que puedan efectuar el
trabajo constituye generalmente la solución menos costosa y más confiable. Por
tanto, el eslabonamiento de cuatro barras debe considerarse dentro de las
primeras soluciones para problemas de control de movimiento que hay que
investigar. La condición de Grashof es una relación muy simple que pronostica
el comportamiento de rotación o rotabilidad de las inversiones de un
eslabonamiento de cuatro barras con base sólo en las longitudes de eslabón [2].
S
= longitud del eslabón más corto
L
= longitud del eslabón más largo
P = longitud de un eslabón
restante
Q = longitud de
otro eslabón restante
S + L ≤ P * Q
Si el eslabonamiento es de
Grashof y por lo menos un eslabón será capaz de realizar una revolución
completa con respecto al plano de fijación. A ésta se le llama cadena
cinemática de clase I. Si esa desigualdad no es cierta, entonces el
eslabonamiento es no Grashof y ningún eslabón podrá realizar una revolución
completa relativa con respecto al plano de fijación. Ésta es una cadena cinemática
de clase II [2].
Los movimientos posibles a partir
de un eslabonamiento de cuatro barras dependerán de la condición de Grashof y
de la inversión elegida. Las inversiones se definirán en relación con el
eslabón más corto. Los movimientos son:
Para el de clase I S + L ≤ P
* Q
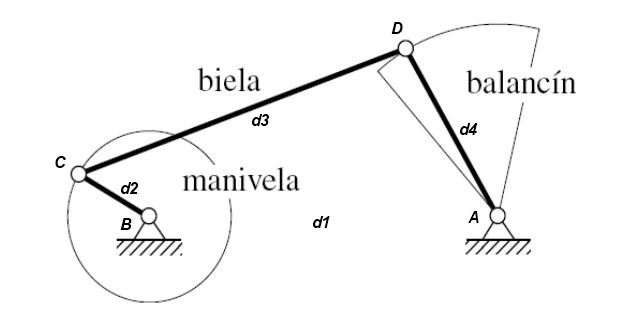
Balancín, en la cual el eslabón
más corto girará completamente y el otro eslabón oscilará pivotado a la
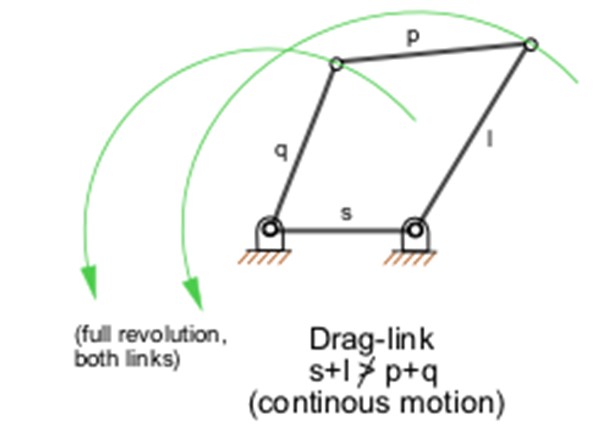
fijación. Si se fija el eslabón más corto se logrará una doble-manivela, en la
que tanto el acoplador como los eslabones pivotados a la fijación realizan
revoluciones completas. Si se fija el eslabón opuesto al más corto se obtendrá
un doble-balancín de Grashof, en el que oscilan los dos eslabones fijos
pivotados a la fijación y sólo el acoplador realiza una revolución completa [2].
Para el caso de clase II I S
+ L ≤ P * Q
Todas las inversiones serán
triples-balancines, en las cuales ningún eslabón puede girar completamente.
Para el caso de clase III S
+ L ≤ P * Q
Designado éste como caso especial
de Grashof y también como cadena cinemática de clase III, todas las inversiones
serán dobles-manivelas, o manivelas-balancín, pero tendrán "puntos de
cambio" dos veces por revolución de la manivela de entrada cuando todos
los eslabones quedan colineales. En estos puntos de cambio el comportamiento de
salida se volverá indeterminado. El comportamiento del eslabonamiento es
entonces impredecible, ya que puede asumir cualquiera de las dos
configuraciones [1].
Clasificación del eslabonamiento
de cuatro barras
 |
Figura.2.- Clasificación completa de Barker de mecanismos de cuatro barras en un plano [2].
|
Referencias
[1] D. H. Myszka, Maquinas y mecanismos, 4th ed.
Pearson Educación de México, S.A. de C.V., 2012, pp. 19-20.
[2] R. Norton, Diseño de maquinaria (2a. ed.), 2nd ed.
McGraw-Hill Interamericana, 2000, pp. 49-56.